수능 수학 합답형에는 출제 원칙이 있는데, 그건 바로 'ㄱ, ㄴ, ㄷ을 모두 풀어야만 답이 도출된다.' 라는 것입니다.
예시를 하나 들어 ㄱ, ㄴ를 풀었고 둘 다 옳은 선지인 것을 확인했다고 가정해 봅시다.
이 상황에서 선지에 ㄱ, ㄴ은 없고 ㄱ, ㄴ, ㄷ밖에 없다면 ㄷ을 풀지 않아도 ㄷ이 옳은 선지라는 것을 알 수 있는데, 평가원은 이런 상황을 지양한다는 것입니다.
평가원은 무려 02수능 가형 이래로 한 번도 이 원칙을 깬 적이 없고, 교육청 역시 최근 시험들에서는 이 원칙이 모두 통했습니다.
그리고 우리는 이 원칙을 역으로 이용해 ㄱ, ㄴ, ㄷ 문제의 답을 유추해 볼 수 있는 것이죠.
물론 이 원칙이 언제 꺠질지 모르고, 그게 여러분이 마주한 시험이 될 수도 있기에,,,선택은 여러분의 몫입니다 ㅎ
이제부터 10년도~20년도 수능/모의고사 기출들로 확인해 봅시다.

10학년도 수능 가형 16번 문제
우선 ㄱ이 옳은 선지라고 가정해 봅시다.
그러면 선택지가 (ㄱ), (ㄱ, ㄴ, ㄷ)밖에 남지 않기에 ㄴ의 정오만 올바르게 판단하면 ㄷ을 판단하지 않아도 답이 바로 도출됩니다.
그러나 앞에서 보았듯이 평가원은 이를 지양하므로, ㄱ은 거짓인 것을 알 수 있습니다.
그럼 (ㄴ), (ㄷ), (ㄴ, ㄷ)이 남는데, 이번엔 ㄴ이 거짓이라고 가정해 봅시다.
그러면 ㄷ을 판단하지 않아도 답이 ㄷ밖에 남지 않으므로 ㄴ은 옳은 선지이고, 결국 답은 ㄴ 또는 ㄴ, ㄷ입니다.
(실제 정답 ㄴ, ㄷ)

11학년도 수능 가형 16번 문제
아까랑 같이 이번엔 ㄱ이 옳지 않은 선지라고 가정해 봅시다.
그럼 선택지가 ㄷ과 ㄴ, ㄷ만 남게 되기에 ㄷ은 판단 과정 없이 옳은 선지임이 도출되므로 ㄱ이 옳은 선지인 것을 알 수 있습니다.
이러면 선택지가 (ㄱ), (ㄱ, ㄴ), (ㄱ, ㄴ, ㄷ)가 남고, 이 상황에서 ㄴ이 옳지 않은 선지라고 가정해 봅시다.
그럼 선택지가 ㄱ 하나만 남기에 ㄷ은 판단 과정 없이 옳지 않은 선지임이 도출되므로 ㄴ도 옳은 선지임을 알 수 있습니다.
따라서 결국 답은 ㄱ, ㄴ 혹은 ㄱ, ㄴ, ㄷ입니다.
(실제 답은 ㄱ, ㄴ)

12학년도 수능 나형 18번
ㄱ이 옳지 않은 선지라면 답이 ㄴ, ㄷ밖에 남지 않기에 ㄱ은 옳은 선지입니다.
ㄴ이 옳은 선지라면 답은 (ㄱ, ㄴ), (ㄱ, ㄴ, ㄷ)이 될 수 있습니다.
ㄴ이 옳지 않은 선지라면 답은 (ㄱ), (ㄱ, ㄷ)이 될 수 있습니다.
따라서 (ㄱ), (ㄱ, ㄴ), (ㄱ, ㄷ), (ㄱ, ㄴ, ㄷ) 모두 답이 될 수 있습니다.
(실제 답은 ㄱ, ㄷ)

13학년도 수능 나형 20번
ㄱ이 옳지 않은 선지라면 답이 ㄴ밖에 남지 않기에 ㄱ은 옳은 선지입니다.
ㄴ이 옳은 선지라면 답은 (ㄱ, ㄴ), (ㄱ, ㄴ, ㄷ)이 될 수 있습니다.
ㄴ이 옳지 않은 선지라면 답은 (ㄱ), (ㄱ, ㄷ)이 될 수 있습니다.
따라서 (ㄱ), (ㄱ, ㄴ), (ㄱ, ㄷ), (ㄱ, ㄴ, ㄷ) 모두 답이 될 수 있습니다.
(실제 답은 ㄱ, ㄷ)

14학년도 수능 나형 19번
ㄱ이 옳지 않은 선지라면 답은 ㄴ 또는 ㄷ이기에 ㄴ의 정오 판단만으로 답을 바로 알 수 있고, 따라서 ㄱ은 옳은 선지입니다.
ㄴ이 옳지 않은 선지라면 ㄱ, ㄷ이 답인 것을 바로 알 수 있으므로 ㄴ도 옳은 선지입니다.
따라서 답은 (ㄱ, ㄴ), (ㄱ, ㄴ, ㄷ) 중 하나인 것을 알 수 있습니다.
(실제 답은 ㄱ, ㄴ, ㄷ)

15학년도 수능 나형 19번
ㄱ이 옳지 않은 선지라면 ㄷ이 옳은 선지인 것을 바로 알 수 있으므로 ㄱ은 옳은 선지입니다.
ㄴ이 옳지 않은 선지라면 ㄱ이 답인 것을 바로 알 수 있으므로 ㄴ도 옳은 선지입니다.
따라서 답은 ㄱ, ㄴ 또는 ㄱ, ㄴ, ㄷ 중 하나입니다.
(실제 답은 ㄱ, ㄴ, ㄷ)

16학년도 수능 나형 18번
ㄱ이 옳지 않은 선지라면 ㄴ은 바로 옳은 선지임이 도출되므로 ㄱ은 옳은 선지입니다.
ㄴ이 옳은 선지라면 ㄱ, ㄴ, ㄷ이 답인 것을 바로 알 수 있으므로 ㄴ은 옳지 않은 선지입니다.
따라서 답은 ㄱ 또는 ㄱ, ㄷ입니다.
(실제 답은 ㄱ, ㄷ)

17학년도 수능 나형 20번
ㄱ이 옳지 않은 선지라면 ㄷ이 옳은 선지임을 바로 알 수 있으므로 ㄱ은 옳은 선지입니다.
ㄴ이 옳지 않은 선지라면 ㄱ이 답인 것이 바로 도출되므로 ㄴ도 옳은 선지입니다.
따라서 답은 ㄱ, ㄴ 또는 ㄱ, ㄴ, ㄷ임을 알 수 있습니다.
(실제 답은 ㄱ, ㄴ, ㄷ)

18학년도 수능 나형 20번
ㄱ이 옳지 않은 선지라면 ㄴ이 옳은 선지임을 바로 알 수 있으므로 ㄱ은 옳은 선지입니다.
ㄴ이 옳은 선지라면 ㄱ, ㄴ, ㄷ이 답인 것을 바로 알 수 있으므로 ㄴ은 옳지 않은 선지임을 알 수 있습니다.
따라서 답은 ㄱ 또는 ㄱ, ㄷ입니다.
(실제 답은 ㄱ, ㄷ)

19학년도 나형 수능 20번
ㄱ이 옳지 않은 선지라면 ㄴ, ㄷ이 답인 것이 바로 확정되므로 ㄱ은 옳은 선지입니다.
ㄴ이 옳은 선지라면 답은 (ㄱ, ㄴ), (ㄱ, ㄴ, ㄷ) 중 하나입니다.
ㄴ이 옳지 않은 선지라면 답은 (ㄱ), (ㄱ, ㄷ) 중 하나입니다.
따라서 답은 (ㄱ), (ㄱ, ㄴ), (ㄱ, ㄷ), (ㄱ, ㄴ, ㄷ) 모두 가능합니다.
(실제 답은 ㄱ, ㄴ, ㄷ)

20학년도 수능 나형 20번
ㄱ이 옳지 않은 선지라면 ㄴ, ㄷ이 답인 것이 바로 도출되므로 ㄱ은 옳은 선지입니다.
ㄴ이 옳은 선지라면 답은 (ㄱ, ㄴ), (ㄱ, ㄴ, ㄷ) 중 하나입니다.ㄴ이 참이라면? 답이 ㄱㄴ 혹은 ㄱㄴㄷ
ㄴ이 옳지 않은 선지라면 답은 (ㄱ), (ㄱ, ㄷ) 중 하나입니다.
따라서 답은 (ㄱ), (ㄱ, ㄴ), (ㄱ, ㄷ) (ㄱ, ㄴ, ㄷ) 모두 가능합니다.
(실제 답은 ㄱ, ㄴ)
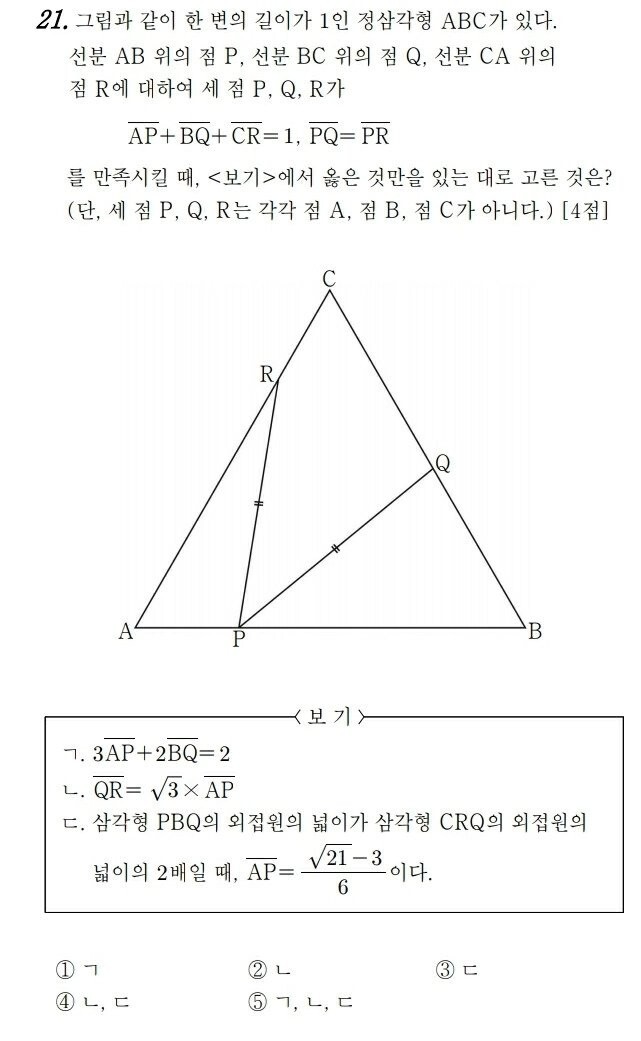
2020년 고2 11모 21번
보너스로 살펴볼 수 있도록 가져와 본 문제입니다.
ㄱ이 옳은 선지라면 ㄴ이 옳은 선지임이 바로 도출되므로 ㄱ은 옳지 않은 선지입니다.
ㄴ이 옳지 않은 선지라면 답은 ㄷ임이 바로 확정되므로 ㄴ은 옳은 선지입니다.
따라서 답은 (ㄴ), (ㄴ, ㄷ) 중 하나인 것을 알 수 있습니다.
(실제 답은 ㄴ, ㄷ)
참고하시고 다들 내일 6평에서 도움 받을 수 있기를 기원합니다!
https://cafe.naver.com/we2you/
위례에듀, 위례지역 중고교 입결, 대... : 네이버 카페
위례, 송파, 성남, 하남지역 초 중 고 및 고입/대입 교육정보 및 진학정보 소통을 위한카페, 학부모소통방
cafe.naver.com
'위례에듀' 카테고리의 다른 글
| 2025년 수시전형 요약 정리(학생부, 논술, 의치약한수) (1) | 2023.05.31 |
|---|---|
| 2023 N제 수1편 1부 (오르비 퍼플스타) (2) | 2023.05.31 |
| 2024 정시 선택과목 지정현황 (이과, 의예과) (4) | 2023.05.31 |
| 2024 수시적정라인 성균관대(학교장추천, 계열모집, 학과모집) (1) | 2023.05.30 |
| 2024 연세대학교 수시모집요강 (0) | 2023.05.30 |