





안녕하세요? 학생들 사이에서 이번 4월 교육청 모의고사가 상당히 까다로웠다는 얘기가 많은 것 같습니다.
이번 4월 교육청 모의고사는 개정교육과정 적용 이후 상당히 쉬워진 최근 수능/평가원 모의고사보다 한 차원
높은 난이도의, 마치 개정교육과정 이전의 변별력 높았던 수능 문제를 보는 듯한 느낌이었습니다.
그래서 기존 평가원이나 교육청 모의고사보다 체감난이도가 상당히 상승했던 듯 하고, 특히 전통적인 킬러
번호인 22번 뿐만 아니라 그동안 상대적으로 무난하게 출제되었던 미적분 28, 29, 30번 라인의 난이도가
상당한 편이라 대부분 미적분을 선택하는 이과 학생들이 꽤 당황스러웠을 듯 합니다.
특히 미적분 킬러문제인 30번 문제는 예전의 어려운 수능 때의 30번을 연상하게 하는 상당한 난이도라서
만약 앞부분에서 시간을 많이 소비했다면 시간 부족으로 인해 제대로 풀기가 어려웠을 듯 합니다.
먼저 20번 수열 준킬러는 상당히 쉬웠습니다. 공차가 양수이고 8번째 항이 0임을 이용하면 쉽게 풀리는 문제였습니다.
21번 역시 코사인 법칙을 적용하면 선분 OP와 OQ가 이차방정식의 두 근이라는 사실을 알 수 있고, 이를 통해
외접원을 그린 뒤 원주각을 이용하면 간단히 풀리는 삼각함수 준킬러 문제였습니다.
22번 킬러 문제부터가 문제인데, 절댓값 기호가 몇 번이나 등장하고 적분 기호도 있어서 문과 학생들의 경우에는
문제 분석 자체가 안 되는 경우도 많았을 듯 하고, 문제 분석만 되면 구간을 나누고 그래프를 그린 후
그 특성을 이용해 쉽게 풀 수 있는 문제였지만 시험장에서의 잔뜩 긴장된 상황을 생각하면 발상하기가 그리
쉽지만은 않았을 듯 합니다.
27번 준킬러 역시 원주각의 성질을 이용하면 쉽게 풀리는 문제였는데, 28번 프랙탈 준킬러부터가
문제였을 듯 합니다.
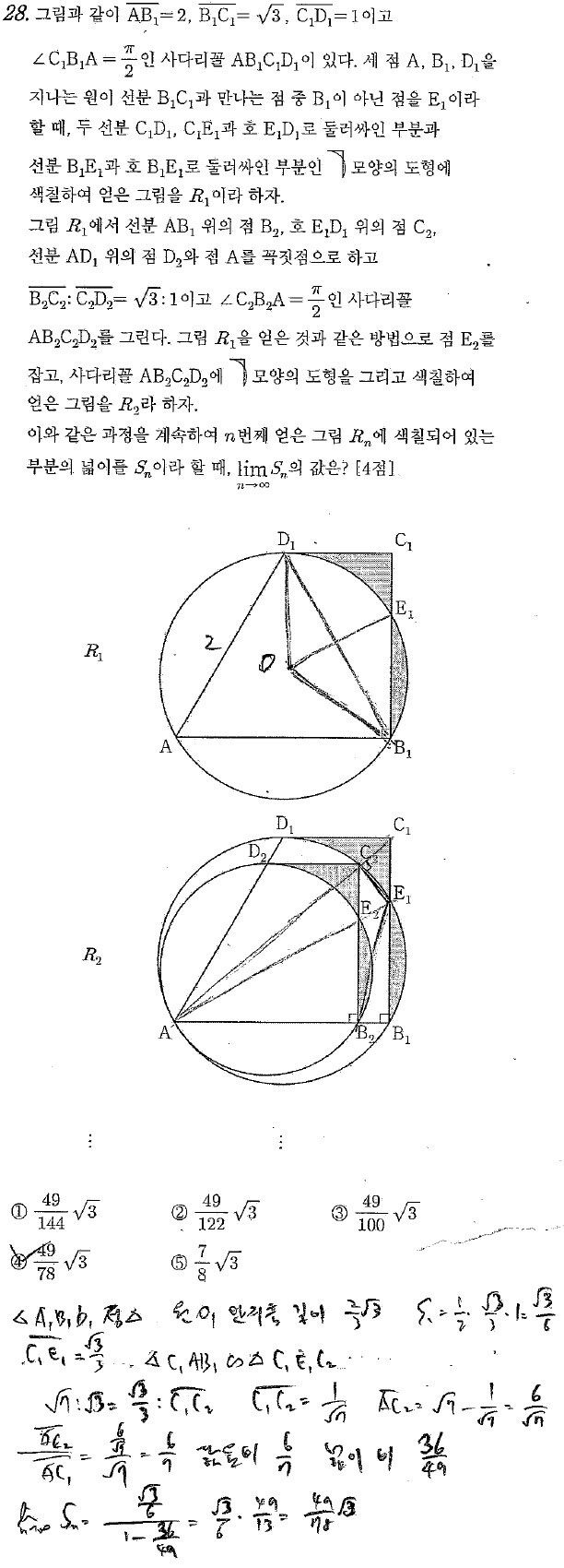
28번 문제는 삼각형 C_1 A B_1 과 C_1 E_1 C_3 가 닮음임이 보이면 바로 풀 수 있는 문제였는데,
만약 이것이 직관적으로 보이지 않았다면 상당한 시간 허비와 함께 당황스러움을 유발할 수 있는,
보기에 따라서는 굉장히 까다로울 수도 있는 문제였습니다.
29번 문제는 접선의 성질을 이용해 원의 중심과 점 O를 잇는 선분이 각의 이등분선임을 파악하고,
수선을 내린 후 삼각함수를 적용하면 풀리는 문제였는데 역시 문제에 주어진 도형이 직관적으로
보이지 않으면 체감 난이도가 확 올라가는 문제였습니다.
30번 미적분 킬러 문제가 가장 어려웠는데, 일단 그래프를 그린 후 x좌표가 정수인 점들에서의
함숫값들을 구하면 되는데 g(x)에 이미 한 번 극한 기호가 들어가고 그 다음에 또다시 극한 기호가
등장해서 많은 학생들이 멘붕에 빠졌을 듯 합니다. 특히 x좌표가 정수일 때 짝수냐 홀수냐에 따라서
함숫값이 달라지는데, 홀수인 경우에는 g(x) 값이 우미분계수의 두 배가 아니라 0이 되어버리는
트릭(유사미분계수) 때문에 오답이 나온 경우도 있었을 듯 합니다. 단순히 미적분 공식에 의한 계산으로
풀리는 문제가 아니라 미분계수의 정의과 개념을 완벽하게 숙지하고 있어야 정답을 구할 수 있는
문제로 풀었더라도 오답이 나오는 경우도 많았을 것 같습니다.
사실 문제 하나하나만 살펴 보면 30번과 22번을 제외하고는 그렇게까지 어려운 정도는 아니었는데,
문제는 시험장에서의 긴장된 상황 속에서 직관적으로 접근법을 찾아내지 못하면 그 체감 난이도는
기하급수적으로 상승할 수 있다는 것이었습니다.
만약 이번 시험에서 기대 이하의 저조한 성적을 받았다면 그동안의 틀에 박힌 공부 방법에서 벗어나
좀 더 심도 있는 문제들과 특히 최근 2~3년간의 쉬운 30번 킬러 문제들 뿐만이 아니라 예전 어려운
수능 시절의 킬러 문제들까지 최대한 많이 풀어보고 단단하게 공부해 두는 것이 앞으로의 평가원이나
실전 수능에서 고득점을 할 수 있는 유일한 길이 아닐까 합니다.
(교육청에서 배부한 공식 해설지가 상당히 조잡한 관계로 직접 손으로 푼 킬러문제 해설을 첨부합니다.)
'위례에듀' 카테고리의 다른 글
| 의학계열 입학설명회 참석 후기 (1) | 2023.05.13 |
|---|---|
| 고교학점제 전면시행 어떻게? 알쏭달쏭 고교학점제 한눈에 알아보기 (3) | 2023.05.13 |
| 서울대 의대 입학생 학부모의 입학자료집 (0) | 2023.05.13 |
| 2025년 교대, 이공계, 계약학과 수시전형 (0) | 2023.05.13 |
| 독서 배경지식 경제용어 300선 (0) | 2023.05.13 |